M203 20260117 Exponents and Logarithms
1. Exponential Function Basics
2b) Find $t$ if $\LARGE 3^{27^t} = 27^{3^t}$
$\LARGE a^{b^c}$ cannot be simplified
2a) Find $x$ if $\LARGE 5^{x^2-3} = 25^x$
2c) Find all values of y such that $4^y – 12*2^y =-32$
2. Logarithms Basics
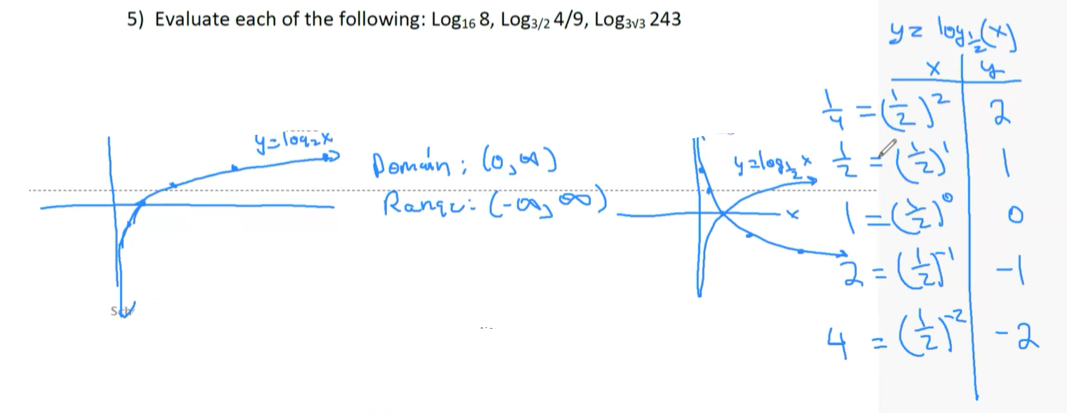
1) Find the domain and range of $f(x) = \log_2 x$. Graph $y = \log_2 x$ and $y = \log_{1/2} x$.
2 ) Solving the inequalities:
$\log_4 (2x-3) > 2$
$\log_{1/5} x > 3$
- increasing function preserves sign of inequality
- decreasing function flips sign of inequality
4 ) Let $x = \log_4 128$, Find $4^x$, $2^x$, Find $x$.
38:43
3b )Find the domain of $f(x) = \log_{1/2} \bigl( \log_5 (\log_{1/3} x) \bigr)$.

3a ) Find the domain of $g(x) = \log_{1/2} (\log_3 x)$.
Find the range of $g(x) = \log_{1/2} (\log_3 x)$.
Find the range of $f(x) = \log_{1/2} \bigl( \log_5 (\log_{1/3} x) \bigr)$.
Change of base can solve 99% of logarithm problems
5)Evaluate each of the following:
$\log_{16} 8$,
$\log_{3/2} \frac{4}{9}$,
$\log_{3\sqrt{3}} 243$
3. Logarithmic Identities
- $\LARGE \log_a(b^c) = c \cdot \log_a b$
- $\LARGE \log_{a^n}(b^n) = \log_a b$
- $\LARGE \log_a b + \log_a c = \log_a (b c)$
- $\LARGE \log_a b - \log_a c = \log_a \left(\dfrac{b}{c}\right)$
- $\LARGE \log_a b \times \log_b c = \log_a c$
- $\LARGE \log_c b = \dfrac{\log_a b}{\log_a c}$
- $\LARGE \log_c b = \dfrac{1}{\log_b c}$
2 ) Evaluate:
- $\log_2 8 \cdot \log_8 64$
- $\dfrac{4}{\log_{10} 5} - \dfrac{2}{\log_4 5}$
- $\log_3 \left( 27^{2007} \right)$
- $\log_2 \frac{2}{3} + \log_2 6$
- $(\log_2 5)(\log_5 12) + (\log_2 7)\left( \log_7 \frac{8}{3} \right)$
- $\dfrac{\log_2 125}{\log_2 25}$
- $\dfrac{2^{\log_4 108}}{2^{\log_4 3}}$
4 ) Find all values of $x$:
$2 \log_3 (x+4) - \log_3 (4x-11) = 2$
Once you find a solution, you actually need to go back and check to make sure your solutions are not extraneous.
For $\log_3 (x+4)$, we need $x+4 > 0 \implies \mathbf{x > -4}$
For $\log_3 (4x-11)$, we need $4x-11 > 0 \implies \mathbf{x > 2.75}$
5 ) Find all ordered pairs of real numbers $(x, y)$ that satisfy the system of equations:
$\log_{10} \left( \dfrac{x^3}{y^4} \right) = 5$
$\log_{10} \left( x^2 \times y^5 \right) = 11$
14 ) Suppose that $p$ and $q$ are positive numbers for which $\log_9 p = \log_{12} q = \log_{16} (p+q)$.
What is the value of $\dfrac{q}{p}$?
18 ) Find all $x$ such that $\LARGE x^{\log_{10} x} = \dfrac{x^3}{100}$
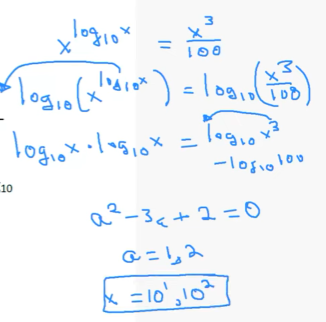
22 ) What is the value of the expression $\dfrac{1}{\log_2 100!} + \dfrac{1}{\log_3 100!} + \dots + \dfrac{1}{\log_{100} 100!}$?